Rectas tangentes a una circunferencia
De Wikillerato
(→Rectas tangentes a una circunferencia pasando por un punto exterior a la circunferencia) |
|||
| Línea 10: | Línea 10: | ||
Para trazar la recta tangente a una circunferencia de centro O por un punto P exterior a la misma, debe tenerse en cuenta que si T es el punto de tangencia buscado entonces el triángulo POT debe ser rectángulo en T, puesto que el radio OT es perpendicular a la tangente PT según se dedujo antes. En consecuencia, el punto de tangencia T deberá estar situado, además de sobre la propia circunferencia, sobre el [[arco capaz]] del ángulo recto con respecto al segmento PO. Recordando que el arco capaz del ángulo recto es la semicircunferencia que tiene por diámetro al segmento con respecto al cual se quiere trazar el arco capaz, la resolución del problema comprenderá los siguientes pasos: | Para trazar la recta tangente a una circunferencia de centro O por un punto P exterior a la misma, debe tenerse en cuenta que si T es el punto de tangencia buscado entonces el triángulo POT debe ser rectángulo en T, puesto que el radio OT es perpendicular a la tangente PT según se dedujo antes. En consecuencia, el punto de tangencia T deberá estar situado, además de sobre la propia circunferencia, sobre el [[arco capaz]] del ángulo recto con respecto al segmento PO. Recordando que el arco capaz del ángulo recto es la semicircunferencia que tiene por diámetro al segmento con respecto al cual se quiere trazar el arco capaz, la resolución del problema comprenderá los siguientes pasos: | ||
| - | + | ||
# Hallar el punto medio M del segmento PO | # Hallar el punto medio M del segmento PO | ||
# Trazar la circunferencia de centro M que pasa por P y por O | # Trazar la circunferencia de centro M que pasa por P y por O | ||
Revisión de 10:48 24 ago 2008
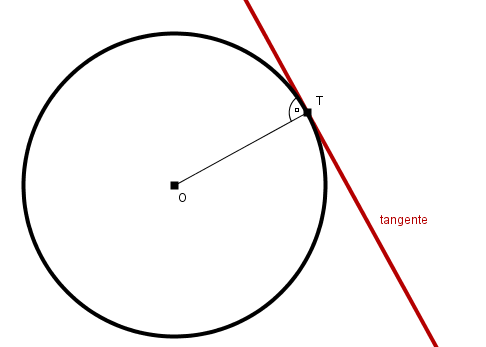
Recta tangente a una circunferencia en un punto de la misma
La recta tangente a una circunferencia de centro O que pasa por un punto T de la misma es la recta perpendicular al radio OT que pasa por el punto T.
Esto ha de ser así porque la perpendicular a una recta trazada desde un punto exterior a la misma indica la menor distancia posible desde dicho punto a la recta. Si el radio OT no fuese perpendicular a la tangente en T, la verdadera perpendicular a la tangente trazada por O cortaría a la tangente en un punto T', de manera que la distancia |OT'| sería inferior a la distancia |OT|. Como la distancia |OT| es el radio de la circunferencia, T' sería un punto del interior de la circunferencia, lo cual se contradice con que la recta sea tangente a la circunferencia.
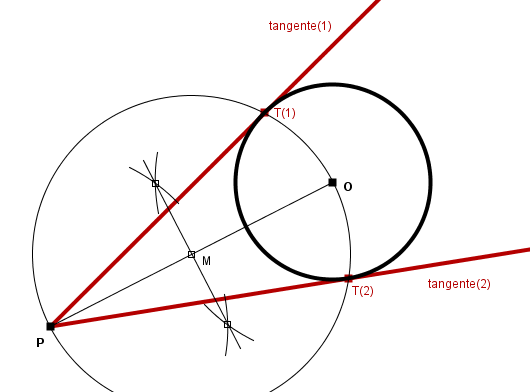
Rectas tangentes a una circunferencia pasando por un punto exterior a la circunferencia
Para trazar la recta tangente a una circunferencia de centro O por un punto P exterior a la misma, debe tenerse en cuenta que si T es el punto de tangencia buscado entonces el triángulo POT debe ser rectángulo en T, puesto que el radio OT es perpendicular a la tangente PT según se dedujo antes. En consecuencia, el punto de tangencia T deberá estar situado, además de sobre la propia circunferencia, sobre el arco capaz del ángulo recto con respecto al segmento PO. Recordando que el arco capaz del ángulo recto es la semicircunferencia que tiene por diámetro al segmento con respecto al cual se quiere trazar el arco capaz, la resolución del problema comprenderá los siguientes pasos:
- Hallar el punto medio M del segmento PO
- Trazar la circunferencia de centro M que pasa por P y por O
- Los puntos de corte de la circunferencia anterior (arco capaz del ángulo recto) con la circunferencia de centro O son los puntos de tangencia buscados. Las rectas tangentes serán las que pasen por P y estos puntos de tangencia
Dadas las dos posibles posiciones del arco capaz del ángulo recto (semicircunferencia a uno u otro lado del segmento PO, que en conjunto forman la circunferencia completa), habrá asimismo dos puntos de tangencia posibles y, por lo tanto, dos rectas diferentes tangentes a la circunferencia y que pasan por el punto exterior P. Ambas rectas, así como los puntos de tangencia, son simétricas con respecto a la recta PO.
Tweet