Navegación
Rango de una matriz
De Wikillerato
En una matriz
![\left(
</p>
<pre> \begin{array}[c]{cccc}
a_{11 }& a_{12} & \ldots & a_{1n}
\\
a_{21 }& a_{22} & \ldots & a_{2n}
\\
\vdots & \vdots & \ddots & \vdots
\\
a_{m1 }& a_{m2} & \ldots & a_{mn}
\end{array}
</pre>
<p>\right)](/images/math/math-2b93b39c0505fe91a8bdffdcb317c676.png "\left(
</p>
<pre> \begin{array}[c]{cccc}
a_{11 }& a_{12} & \ldots & a_{1n}
\\
a_{21 }& a_{22} & \ldots & a_{2n}
\\
\vdots & \vdots & \ddots & \vdots
\\
a_{m1 }& a_{m2} & \ldots & a_{mn}
\end{array}
</pre>
<p>\right)")
podemos considerar sus filas y sus columnas como vectores.
El rango de una matriz es el número de filas o de columnas linealmente independientes que tiene esa matriz.
El rango de una matriz es, por tanto, siempre menor igual que su numero de filas, y tambien, menor igual que su numero de columnas. Las unicas matrices con rango 0 son las matrices nulas.
El rango de una matriz se puede calcular mediante el método de Gauss o usando menores.
Calculo del rango de una matriz por el método de Gauss
Este metodo consiste en transformar la matriz
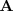en una matriz triangular superior mediante ciertas
operaciones
elementales con sus filas.
Una vez que se obtiene una matriz triangular superior a partir de la matriz
,
el rango de
lo obtenemos restando al número de filas de
el número de filas con todos sus elementos iguales a cero en la matriz
triangular superior obtenida.
