Propiedades de la integral definida
De Wikillerato
La integral de la suma de dos funciones es igual a la suma de las integrales de las funciones:
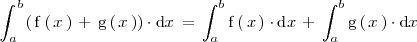
La integral del producto de un número realpor una función es igual al producto de
por la integral de dicha función:
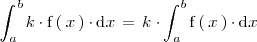
En una integral definida el limite superior de integraci\'on puede ser menor que el limite inferior de integraci\'on y
[Unparseable or potentially dangerous latex formula. Error 3 ]
Si hacemos
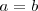 en la igualdad anterior se tiene que
en la igualdad anterior se tiene que
[Unparseable or potentially dangerous latex formula. Error 3 ]
como el único número que coincide con su opuesto es el cero, llegamos a la conclusión de que
[Unparseable or potentially dangerous latex formula. Error 3 ]
para cualquier número real
 .
.
Dados tres números reales cualesquiera,
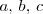 se tiene que:
se tiene que:
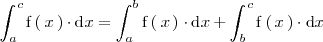
Si en el intervalo
![\left[ \, a, \, b \, \right]
\left[ \, a, \, b \, \right]](/images/math/math-bd2e5d8941aab87895e8817c63d00863.png) la función
la función
 es mayor o igual que la función
es mayor o igual que la función
 entonces
entonces
[Unparseable or potentially dangerous latex formula. Error 3 ]
Si en el intervalo
![\left[ \, a, \, b \, \right]
\left[ \, a, \, b \, \right]](/images/math/math-bd2e5d8941aab87895e8817c63d00863.png) la función
la función
 es mayor que la función
es mayor que la función
 entonces
entonces
[Unparseable or potentially dangerous latex formula. Error 3 ]



