Ejercicios:Matriz inversa
De Wikillerato
Esta es la página de Ejercicios del artículo "Matriz inversa".
Aquí puedes plantear enunciados de problemas o cuestiones de desarrollo para que otros usuarios respondan.
Atención: es necesario iniciar sesión para poder editar esta página.
Ejercicio 1
Se consideran las matrices 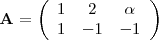 y
y 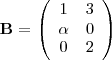 donde
donde 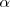 es un número real.
es un número real.
- Encontrar los valores de
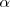 para los que
para los que 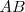 es invertible.
es invertible.
- Encontrar los valores de
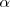 para los que
para los que 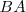 es invertible.
es invertible.
- Dados
 y
y 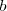 , números reales cualesquiera, ¿puede ser el sistema
, números reales cualesquiera, ¿puede ser el sistema
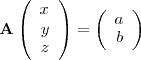 compatible determinado?
compatible determinado?
Ejercicio 2
Dada la matriz:
A = 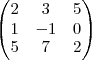
Contesta a las siguientes cuestiones:
1. ¿Qué dimensión tiene?
2. ¿Es simétrica? Razona tu respuesta.
3. Calcula su determinante.
4. ¿Es posible obtener su inversa? Justifica tu respuesta y, en caso afirmativo, obten su matriz inversa.



