Dudas:Ecuaciones del plano

De Wikillerato

Esta es la página de Dudas del artículo "Ecuaciones del plano".
Puedes hacer preguntas aquí sobre el tema que trata si no has entendido algo o quieres saber más.
Atención: es necesario iniciar sesión para poder editar esta página.

Ecuacion general del plano

Cómo se plantea la ecuacion general del plano a partir de la ecuacion normal??????

Isabel pozo (Discutir)

00:03 27 nov 2011

Ver código fuente

Pues como se explica en la entrada de wikillerato Ecuaciones del plano, un plano está perfectamente definido, si conoces 3 puntos que pertenecen a ese plano. A partir de esos 3 puntos, existen 4 formas de expresar un plano en forma de ecuaciones:

Ecuación en forma vectorial
Ecuación en forma paramétrica
Ecuación en forma general
Ecuación normal

Si partes de la ecuación normal de un plano: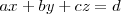

$ax + by + cz = d$

puedes hayar fácilmente 3 puntos que pertenezcan a dicho plano, por ejemplo, si tienes la ecuacion normal de un plano cualquiera: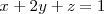

$x + 2y + z = 1$

puedes elegir valores x e y, para después calcular z: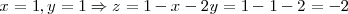

$x = 1, y = 1 \Rightarrow z = 1 - x - 2y = 1 - 1 - 2 = -2$

por lo que ya tendríamos un punto que pertenece al plano,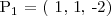

$$P_{1}$ = ( 1, 1, -2)$

Si hacemos lo mis otras dos veces, obtenemos los tres puntos que definen mi plano: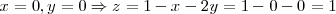

$x = 0, y = 0 \Rightarrow z = 1 - x - 2y = 1 - 0 - 0 = 1$

$$P_{2}$ = ( 0, 0, 1)$

$x = -1, y = -1 \Rightarrow z = 1 - (-1) - 2(-1) = 1 + 1 + 2 = 4$

$$P_{3}$ = ( -1, -1, 4)$

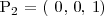
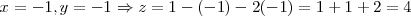
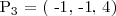
A partir de estos tres puntos puedes calcular 2 vectores que pertenecen al plano: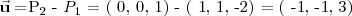

$\vec{\mathbf{u}} = $P_{2}$ - $P_{1}$ = ( 0, 0, 1) - ( 1, 1, -2) = ( -1, -1, 3)$

$\vec{\mathbf{u}} = $P_{3}$ - $P_{1}$ = ( -1, -1, 4) - ( 1, 1, -2) = ( -2, -2, 2)$

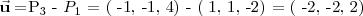
Y siguiendo los pasos que se explican en la página Ecuaciones del plano, puedes hayar la ecuanción del plano en forma general, ya que se define a partir de un punto 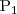$P_{1}$ y 2 vectores $\vec{\mathbf{u}}$ y $\vec{\mathbf{v}}$ .

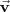Para hayar dicha ecuación sólo hay que sustituir nuestros valores en el siguiete determinante e igualarlo a cero

$\left| </p> <pre> \begin{array}[c]{rcl} x \, - \, x_0 & u_x & v_x \\ y \, - \, y_0 & u_y & v_y \\ z \, - \, z_0 & u_z & v_z \\ \end{array} </pre> <p>\right| = 0$

Por lo que desarroyando el siguiente determinante hayarías dicha ecuanción:

$\left| </p> <pre> \begin{array}[c]{rcl} x \, - \, 1 & -1 & -2 \\ y \, - \, 1 & -1 & -2 \\ z \, + \, 2 & \ 3 & \ 2 \\ \end{array} </pre> <p>\right| = 0$