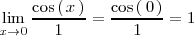Indeterminaciones
De Wikillerato
(Página nueva: %% {{{ =indeterminaciones ==Introducción== <br/> Muchas de las funciones que se ven en bachillerato son continuas en toda la recta real o en casi todos los puntos de su dominio. ...) |
|||
| Línea 1: | Línea 1: | ||
| - | + | ||
==Introducción== | ==Introducción== | ||
| Línea 5: | Línea 5: | ||
<br/> | <br/> | ||
| - | Muchas de las funciones que se ven en bachillerato son continuas en toda la recta real o en casi todos los puntos de su dominio. | + | Muchas de las funciones que se ven en bachillerato son [[Continuidad de una función|continuas]] en toda la recta real o en casi todos los puntos de su dominio. |
<br/> | <br/> | ||
| Línea 21: | Línea 21: | ||
\mathrm{f} | \mathrm{f} | ||
</math> | </math> | ||
| - | es continua en | + | es continua en |
| + | <math> | ||
| + | x_0 \in \mathbb{R} | ||
| + | </math>, | ||
| + | el limite de | ||
<math> | <math> | ||
\mathrm{f} | \mathrm{f} | ||
| Línea 31: | Línea 35: | ||
tiende a | tiende a | ||
<math> | <math> | ||
| - | x_0 | + | x_0 |
</math> | </math> | ||
se puede calcular simplemente evaluando | se puede calcular simplemente evaluando | ||
| Línea 75: | Línea 79: | ||
| - | Por ejemplo, si | + | Por ejemplo, si existen los limites |
| + | <center> | ||
<math> | <math> | ||
| - | \mathrm{f} | + | \lim_{x \to x_0} \mathrm{g} \left( \, x_0 \, \right), \, |
| + | \lim_{x \to x_0} \mathrm{f} \left( \, x_0 \, \right) | ||
</math> | </math> | ||
| + | </center> | ||
y | y | ||
| + | <center> | ||
<math> | <math> | ||
| - | \mathrm{g} | + | \lim_{x \to x_0} \mathrm{g} \left( \, x_0 \, \right) \neq 0 |
</math> | </math> | ||
| - | + | </center> | |
| + | entonces se puede calcular el límite | ||
| + | <center> | ||
<math> | <math> | ||
| - | x_0 | + | \lim_{x \to x_0} \frac{\mathrm{f} \left( \, x \, \right)}{\mathrm{g}\left( \, x |
| + | \, \right)} | ||
</math> | </math> | ||
| - | | + | </center> |
| - | + | dividiendo | |
| - | + | ||
<math> | <math> | ||
| - | \mathrm{ | + | \lim_{x \to x_0} \mathrm{f}\left( \, x \, \right) |
</math> | </math> | ||
| - | </ | + | entre |
| - | + | <math> | |
| + | \lim_{x \to x_0} \mathrm{g}\left( \, x \, \right)} | ||
| + | </math>: | ||
| + | |||
<center> | <center> | ||
<math> | <math> | ||
\lim_{x \to x_0} \frac{\mathrm{f} \left( \, x \, \right)}{\mathrm{g}\left( \, x | \lim_{x \to x_0} \frac{\mathrm{f} \left( \, x \, \right)}{\mathrm{g}\left( \, x | ||
| - | \, \right)} = \frac{\mathrm{f}\left( | + | \, \right)} = \frac{\displaystyle \lim_{x \to x_0} \mathrm{f}\left( \, x \, |
| - | + | \right)}{\displaystyle \lim_{x \to x_0} \mathrm{g}\left( \, x \, \right)} | |
</math> | </math> | ||
</center> | </center> | ||
¿Pero que sucede cuando | ¿Pero que sucede cuando | ||
<math> | <math> | ||
| - | \mathrm{g} \left( \, | + | \lim_{x \to x_0} \mathrm{g} \left( \, x \, \right) = 0 |
</math>? | </math>? | ||
| Línea 113: | Línea 126: | ||
<br/> | <br/> | ||
| - | #1. <math> \mathrm{f} \left( \, x \, \right) \neq 0 </math>, o bien | + | #1. <math> \lim_{x \to x_0} \mathrm{f} \left( \, x \, \right) \neq 0 </math>, o bien |
<br/> | <br/> | ||
| - | #2. <math> \mathrm{f} \left( \, x \, \right) = 0 | + | #2. <math> \lim_{x \to x_0} \mathrm{f} \left( \, x \, \right) = 0 </math>. |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | </math>. | + | |
<br/> | <br/> | ||
| - | En | + | En este último caso, de exisir el limite |
<center> | <center> | ||
<math> | <math> | ||
| Línea 138: | Línea 140: | ||
</math> | </math> | ||
</center> | </center> | ||
| - | de otra manera. | + | se ha de calcular de otra manera. |
<br/> | <br/> | ||
| Línea 156: | Línea 158: | ||
<math> | <math> | ||
x - x_0 | x - x_0 | ||
| - | </math> | + | </math>, |
| - | + | cuantas veces sea posible. | |
| - | posible | + | |
<br/> | <br/> | ||
| Línea 172: | Línea 173: | ||
</math> | </math> | ||
</center> | </center> | ||
| - | + | con | |
<center> | <center> | ||
<math> | <math> | ||
| Línea 216: | Línea 217: | ||
</math> | </math> | ||
| | ||
| - | nos queda que | + | una vez y luego otra, nos queda que |
<center> | <center> | ||
<math> | <math> | ||
\lim_{x \to 1} \frac{\mathrm{f} \left( \, x \, \right)}{\mathrm{g}\left( \, x | \lim_{x \to 1} \frac{\mathrm{f} \left( \, x \, \right)}{\mathrm{g}\left( \, x | ||
| - | \, \right)} = \lim_{x \to 1} \frac{x^2 - 1}{x^2 + x - 2} | + | \, \right)} = \lim_{x \to 1} \frac{x^2 - 1}{x^2 + x - 2} = |
| + | \lim_{x \to 1} \frac{x + 1}{x - 2} = \frac{1 + 1}{1 - 2} = \frac{2}{-1} = -2 | ||
</math> | </math> | ||
</center> | </center> | ||
| - | + | ||
| + | Todas esas divisiones se puede hacer por la [[Regla de Ruffini|regla de Ruffini]]. | ||
<br/> | <br/> | ||
| Línea 239: | Línea 242: | ||
\mathrm{g} | \mathrm{g} | ||
</math> | </math> | ||
| - | se puede utilizar la regla de L | + | se puede utilizar la '''''regla de L'Hôpital''''': |
| + | |||
| + | <br/> | ||
| + | |||
Si existe | Si existe | ||
<center> | <center> | ||
| Línea 257: | Línea 263: | ||
\right)}{\mathrm{g}^\prime \left( \, x \, \right)} | \right)}{\mathrm{g}^\prime \left( \, x \, \right)} | ||
</math> | </math> | ||
| - | |||
donde | donde | ||
<math> | <math> | ||
| Línea 284: | Línea 289: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \lim_{x \to 0} \frac{sen \left( \, x \, \right)}{x} | + | \lim_{x \to 0} \frac{\mathrm{sen} \left( \, x \, \right)}{x} |
</math> | </math> | ||
</center> | </center> | ||
| Línea 298: | Línea 303: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \frac{\sen \left( \, x \, \right)}{x} | + | \frac{\mathrm{sen} \left( \, x \, \right)}{x} |
</math> | </math> | ||
</center> | </center> | ||
| Línea 305: | Línea 310: | ||
\frac{0}{0} | \frac{0}{0} | ||
</math>. | </math>. | ||
| - | + | ||
| - | Esto | + | <br/> |
| + | |||
| + | Esto NO significa que el limite NO exista, de hecho si derivamos el numerador y | ||
el denominador en | el denominador en | ||
<math> | <math> | ||
| - | \frac{\sen \left( \, x \, \right)}{x} | + | \frac{\mathrm{sen} \left( \, x \, \right)}{x} |
</math> | </math> | ||
obtenemos | obtenemos | ||
| Línea 321: | Línea 328: | ||
tiende a | tiende a | ||
<math> | <math> | ||
| - | + | 0 | |
</math> | </math> | ||
tiende a 1. | tiende a 1. | ||
| Línea 327: | Línea 334: | ||
<br/> | <br/> | ||
| - | Por lo tanto, por la regla de L' | + | Por lo tanto, por la regla de L'Hôpital |
<center> | <center> | ||
<math> | <math> | ||
| - | \lim_{x \to 0} \frac{\sen \left( \, x \, \right)}{x} = | + | \lim_{x \to 0} \frac{\mathrm{sen} \left( \, x \, \right)}{x} = |
\lim_{x \to 0} \frac{\cos \left( \, x \, \right)}{1} = 1 | \lim_{x \to 0} \frac{\cos \left( \, x \, \right)}{1} = 1 | ||
</math> | </math> | ||
| Línea 338: | Línea 345: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \lim_{x \to 0} \frac{\cos \left( \, x \, \right)}{1} = \cos \left( \, 0 \, \right) | + | \lim_{x \to 0} \frac{\cos \left( \, x \, \right)}{1} = |
| + | \frac{\cos \left( \, 0 \, \right)}{1} = 1 | ||
</math> | </math> | ||
| - | </center | + | </center> |
| - | + | [[Categoría:Matemáticas]] | |
Revisión de 16:41 25 ago 2010
Tabla de contenidos |
Introducción
Muchas de las funciones que se ven en bachillerato son continuas en toda la recta real o en casi todos los puntos de su dominio.
Este es el caso de los polinomios, las funciones exponenciales
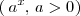 , el coseno, el seno, etc.
, el coseno, el seno, etc.
Si una función
 es continua en
es continua en
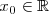 ,
el limite de
,
el limite de
 cuando
cuando
 tiende a
tiende a
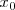 se puede calcular simplemente evaluando
se puede calcular simplemente evaluando
 en
en
 .
.
Ejemplo
Como
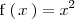 es una función continua en todo
es una función continua en todo
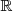 se tiene que
se tiene que
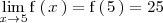
Indeterminación del tipo 0/0
En muchos casos, el limite se calcula utilizando las propiedades de los limites.
Por ejemplo, si existen los limites
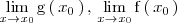
y
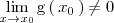
entonces se puede calcular el límite
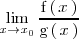
dividiendo
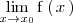 entre
entre
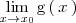 :
:
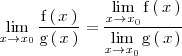
¿Pero que sucede cuando
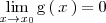 ?
?
Pueden darse dos casos:
- 1.
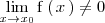 , o bien
, o bien
- 2.
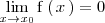 .
.
En este último caso, de exisir el limite
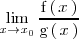
se ha de calcular de otra manera.
Procedimiento 1
Si  y
y
 son polinomios, entonces se puede dividir ambos por
son polinomios, entonces se puede dividir ambos por
 ,
cuantas veces sea posible.
,
cuantas veces sea posible.
Ejemplo
Calculemos el limite
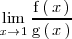
con
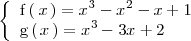
Ambos polinomios,
 y
y
 ,
se anulan en
,
se anulan en
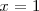 ,
por lo tanto ambos son divisibles por
,
por lo tanto ambos son divisibles por
 .
.
Si dividimos
 y
y
 por
por
 una vez y luego otra, nos queda que
una vez y luego otra, nos queda que
[Unparseable or potentially dangerous latex formula. Error 3 ]
Todas esas divisiones se puede hacer por la regla de Ruffini.
Procedimiento 2
Independientemente de como sean
 y
y
 se puede utilizar la regla de L'Hôpital:
se puede utilizar la regla de L'Hôpital:
Si existe
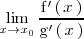
ya sea
 real, infinito o menos infinito, entonces
real, infinito o menos infinito, entonces
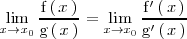 donde
donde
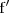 y
y
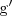 son las derivadas de
son las derivadas de
 y
y
 .
.
Ejemplo
Calculemos
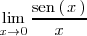
Como la funcion seno y la funcion identidad
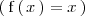 son funciones continuas, lo primero que hacemos es sustituir
son funciones continuas, lo primero que hacemos es sustituir
 por cero en
por cero en
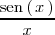
con lo que obtenemos la indeterminación
 .
.
Esto NO significa que el limite NO exista, de hecho si derivamos el numerador y
el denominador en
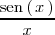 obtenemos
obtenemos
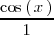 que cuando
que cuando
 tiende a
tiende a
 tiende a 1.
tiende a 1.
Por lo tanto, por la regla de L'Hôpital
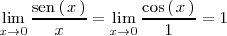
El ultimo límite se calcula teniendo en cuenta que la función coseno es continua