Indeterminaciones
De Wikillerato
(Página nueva: %% {{{ =indeterminaciones ==Introducción== <br/> Muchas de las funciones que se ven en bachillerato son continuas en toda la recta real o en casi todos los puntos de su dominio. ...) |
|||
| (12 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| - | |||
| - | |||
==Introducción== | ==Introducción== | ||
| - | + | Muchas de las funciones elementales que se ven en bachillerato son [[Continuidad de una función|continuas]] en toda la recta real o en casi todos los puntos de su dominio. | |
| - | + | Las funciones elementales son aquellas que se utilizan para construir otras | |
| + | funciones mediante las operaciones con funciones: suma, resta, división, | ||
| + | multiplicación, composición, etc. | ||
| - | + | Son funciones elementales los polinomios, las funciones exponenciales | |
| - | + | ||
| - | + | ||
<math> | <math> | ||
\left( \, a^x, \, a > 0 \right) | \left( \, a^x, \, a > 0 \right) | ||
</math> | </math> | ||
, el coseno, el seno, etc. | , el coseno, el seno, etc. | ||
| - | |||
| - | |||
Si una función | Si una función | ||
| Línea 21: | Línea 17: | ||
\mathrm{f} | \mathrm{f} | ||
</math> | </math> | ||
| - | es continua en | + | es continua en |
| + | <math> | ||
| + | x_0 \in \mathbb{R} | ||
| + | </math>, | ||
| + | el limite de | ||
<math> | <math> | ||
\mathrm{f} | \mathrm{f} | ||
| Línea 31: | Línea 31: | ||
tiende a | tiende a | ||
<math> | <math> | ||
| - | x_0 | + | x_0 |
</math> | </math> | ||
se puede calcular simplemente evaluando | se puede calcular simplemente evaluando | ||
| Línea 42: | Línea 42: | ||
</math>. | </math>. | ||
| - | |||
| - | |||
| - | + | ===Ejemplo 0=== | |
| + | |||
| + | |||
Como | Como | ||
| Línea 64: | Línea 64: | ||
</center> | </center> | ||
| - | + | ||
==Indeterminación del tipo 0/0== | ==Indeterminación del tipo 0/0== | ||
| - | |||
| - | |||
En muchos casos, el limite se calcula utilizando las [[Propiedades de los límites|propiedades de los limites]]. | En muchos casos, el limite se calcula utilizando las [[Propiedades de los límites|propiedades de los limites]]. | ||
| - | + | Por ejemplo, si existen los limites | |
| - | + | <center> | |
| - | + | ||
| - | Por ejemplo, si | + | |
<math> | <math> | ||
| - | \mathrm{f} | + | \lim_{x \to x_0} \mathrm{g} \left( \, x_0 \, \right), \, |
| + | \lim_{x \to x_0} \mathrm{f} \left( \, x_0 \, \right) | ||
</math> | </math> | ||
| + | </center> | ||
y | y | ||
| + | <center> | ||
<math> | <math> | ||
| - | \mathrm{g} | + | \lim_{x \to x_0} \mathrm{g} \left( \, x_0 \, \right) \neq 0 |
</math> | </math> | ||
| - | + | </center> | |
| + | entonces se puede calcular el límite | ||
| + | <center> | ||
<math> | <math> | ||
| - | x_0 | + | \lim_{x \to x_0} \frac{\mathrm{f} \left( \, x \, \right)}{\mathrm{g}\left( \, x |
| + | \, \right)} | ||
</math> | </math> | ||
| - | | + | </center> |
| - | + | dividiendo | |
| - | + | ||
<math> | <math> | ||
| - | \mathrm{ | + | \lim_{x \to x_0} \mathrm{f}\left( \, x \, \right) |
</math> | </math> | ||
| - | </ | + | entre |
| - | + | <math> | |
| + | \lim_{x \to x_0} \mathrm{g}\left( \, x \, \right)} | ||
| + | </math>: | ||
| + | |||
<center> | <center> | ||
<math> | <math> | ||
\lim_{x \to x_0} \frac{\mathrm{f} \left( \, x \, \right)}{\mathrm{g}\left( \, x | \lim_{x \to x_0} \frac{\mathrm{f} \left( \, x \, \right)}{\mathrm{g}\left( \, x | ||
| - | \, \right)} = \frac{\mathrm{f}\left( | + | \, \right)} = \frac{\displaystyle \lim_{x \to x_0} \mathrm{f}\left( \, x \, |
| - | + | \right)}{\displaystyle \lim_{x \to x_0} \mathrm{g}\left( \, x \, \right)} | |
</math> | </math> | ||
</center> | </center> | ||
¿Pero que sucede cuando | ¿Pero que sucede cuando | ||
<math> | <math> | ||
| - | \mathrm{g} \left( \, | + | \lim_{x \to x_0} \mathrm{g} \left( \, x \, \right) = 0 |
</math>? | </math>? | ||
| Línea 113: | Línea 117: | ||
<br/> | <br/> | ||
| - | #1. <math> \mathrm{f} \left( \, x \, \right) \neq 0 </math>, o bien | + | #1. <math> \lim_{x \to x_0} \mathrm{f} \left( \, x \, \right) \neq 0 </math>, o bien |
<br/> | <br/> | ||
| - | #2. <math> \mathrm{f} \left( \, x \, \right) = 0 </math>. | + | #2. <math> \lim_{x \to x_0} \mathrm{f} \left( \, x \, \right) = 0 </math>. |
<br/> | <br/> | ||
| - | En | + | En este último caso, de existir el limite |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<center> | <center> | ||
<math> | <math> | ||
| Línea 138: | Línea 131: | ||
</math> | </math> | ||
</center> | </center> | ||
| - | de otra manera. | + | se ha de calcular de otra manera. |
<br/> | <br/> | ||
| Línea 156: | Línea 149: | ||
<math> | <math> | ||
x - x_0 | x - x_0 | ||
| - | </math> | + | </math>, |
| - | + | cuantas veces sea posible. | |
| - | posible | + | |
<br/> | <br/> | ||
| - | ===Ejemplo=== | + | ===Ejemplo 1=== |
<br/> | <br/> | ||
| Línea 172: | Línea 164: | ||
</math> | </math> | ||
</center> | </center> | ||
| - | + | con | |
<center> | <center> | ||
<math> | <math> | ||
| Línea 216: | Línea 208: | ||
</math> | </math> | ||
| | ||
| - | nos queda que | + | una vez y luego otra, nos queda que |
<center> | <center> | ||
<math> | <math> | ||
\lim_{x \to 1} \frac{\mathrm{f} \left( \, x \, \right)}{\mathrm{g}\left( \, x | \lim_{x \to 1} \frac{\mathrm{f} \left( \, x \, \right)}{\mathrm{g}\left( \, x | ||
| - | \, \right)} = \lim_{x \to 1} \frac{x^2 - 1}{x^2 + x - 2} | + | \, \right)} = \lim_{x \to 1} \frac{x^2 - 1}{x^2 + x - 2} = |
| + | \lim_{x \to 1} \frac{x + 1}{x + 2} = | ||
| + | \frac{\displaystyle \lim_{x \to 1} \left( \, x + 1 \, \right)} | ||
| + | {\displaystyle \lim_{x \to 1} \left( \, x + 2 \, \right)} = | ||
| + | \frac{1 + 1}{1 + 2} = \frac{2}{3} | ||
</math> | </math> | ||
</center> | </center> | ||
| - | + | ||
| + | Todas esas divisiones se puede hacer por la [[Regla de Ruffini|regla de Ruffini]]. | ||
<br/> | <br/> | ||
| Línea 231: | Línea 228: | ||
<br/> | <br/> | ||
| - | + | Tanto si | |
<math> | <math> | ||
\mathrm{f} | \mathrm{f} | ||
| Línea 239: | Línea 236: | ||
\mathrm{g} | \mathrm{g} | ||
</math> | </math> | ||
| - | se puede utilizar la regla de L | + | son polinomios, como si no lo son, se puede utilizar la '''''regla de L'Hôpital''''': |
| + | |||
| + | <br/> | ||
| + | |||
Si existe | Si existe | ||
<center> | <center> | ||
| Línea 252: | Línea 252: | ||
</math> | </math> | ||
real, infinito o menos infinito, entonces | real, infinito o menos infinito, entonces | ||
| + | <center> | ||
<math> | <math> | ||
\lim_{x \to x_0} \frac{\mathrm{f} \left( \, x \, \right)}{\mathrm{g} \left( \, x \, \right)} = | \lim_{x \to x_0} \frac{\mathrm{f} \left( \, x \, \right)}{\mathrm{g} \left( \, x \, \right)} = | ||
| Línea 277: | Línea 278: | ||
<br/> | <br/> | ||
| - | ===Ejemplo=== | + | ===Ejemplo 2=== |
<br/> | <br/> | ||
| Línea 284: | Línea 285: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \lim_{x \to 0} \frac{sen \left( \, x \, \right)}{x} | + | \lim_{x \to 0} \frac{\mathrm{sen} \left( \, x \, \right)}{x} |
</math> | </math> | ||
</center> | </center> | ||
| Línea 298: | Línea 299: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \frac{\sen \left( \, x \, \right)}{x} | + | \frac{\mathrm{sen} \left( \, x \, \right)}{x} |
</math> | </math> | ||
</center> | </center> | ||
| Línea 305: | Línea 306: | ||
\frac{0}{0} | \frac{0}{0} | ||
</math>. | </math>. | ||
| - | + | ||
| - | Esto | + | <br/> |
| + | |||
| + | Esto NO significa que el limite NO exista, de hecho si derivamos el numerador y | ||
el denominador en | el denominador en | ||
<math> | <math> | ||
| - | \frac{\sen \left( \, x \, \right)}{x} | + | \frac{\mathrm{sen} \left( \, x \, \right)}{x} |
</math> | </math> | ||
obtenemos | obtenemos | ||
| Línea 321: | Línea 324: | ||
tiende a | tiende a | ||
<math> | <math> | ||
| - | + | 0 | |
</math> | </math> | ||
tiende a 1. | tiende a 1. | ||
| Línea 327: | Línea 330: | ||
<br/> | <br/> | ||
| - | Por lo tanto, por la regla de L' | + | Por lo tanto, por la regla de L'Hôpital |
<center> | <center> | ||
<math> | <math> | ||
| - | \lim_{x \to 0} \frac{\sen \left( \, x \, \right)}{x} = | + | \lim_{x \to 0} \frac{\mathrm{sen} \left( \, x \, \right)}{x} = |
\lim_{x \to 0} \frac{\cos \left( \, x \, \right)}{1} = 1 | \lim_{x \to 0} \frac{\cos \left( \, x \, \right)}{1} = 1 | ||
</math> | </math> | ||
| Línea 338: | Línea 341: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \lim_{x \to 0} \frac{\cos \left( \, x \, \right)}{1} = \cos \left( \, 0 \, \right) | + | \lim_{x \to 0} \frac{\cos \left( \, x \, \right)}{1} = |
| + | \frac{\cos \left( \, 0 \, \right)}{1} = 1 | ||
</math> | </math> | ||
| - | </center> | + | </center> |
| + | |||
| + | <br/> | ||
| + | |||
| + | ===Ejemplo 3=== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Calculemos el limite del ejemplo 1 utilizando la regla de L'Hôpital y | ||
| + | comprobemos que el resultado es el mismo que obtuvimos utilizando el | ||
| + | procedimiento 1. | ||
| + | <center> | ||
| + | <math> | ||
| + | \lim_{x \to 1} \frac{\mathrm{f} \left( \, x \, \right)}{\mathrm{g}\left( \, x \, \right)} = | ||
| + | \lim_{x \to 1} \frac{\mathrm{f}^\prime \left( \, x \, \right)} | ||
| + | {\mathrm{g}^\prime \left( \, x \, \right)} = | ||
| + | \lim_{x \to 1} \frac{2x}{2x + 1} = \frac{2 \cdot 1}{2 \cdot 1 + 1} = \frac{2}{3} | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ==Indeterminación del tipo infinito/infinito== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Supongamos que queremos calcular el limite de | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \lim_{x \to x_0} \frac{\mathrm{f} \left( \, x \, \right)}{\mathrm{g}\left( \, x | ||
| + | \, \right)} | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | y que | ||
| + | <math> | ||
| + | \lim_{x \to x_0} \mathrm{g}\left( \, x \, \right)} = \infty | ||
| + | </math>. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Puede darse dos casos, o bien: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | #1. <math> \lim_{x \to x_0} \mathrm{f} \left( \, x \, \right) \in \mathbb{R} </math>, o bien | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | #2. <math> \lim_{x \to x_0} \mathrm{f} \left( \, x \, \right) = \infty </math>. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | En el primer caso | ||
| + | <math> | ||
| + | \lim_{x \to x_0} \frac{\mathrm{f} \left( \, x \, \right)}{\mathrm{g}\left( \, x | ||
| + | \, \right)} = 0 | ||
| + | </math>. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | En este segundo caso se dice que se tiene una indeterminación del tipo | ||
| + | <math> | ||
| + | \frac{\infty}{\infty} | ||
| + | </math>. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Veamos a continuación diferentes metodos de calcular limites cuando | ||
| + | se llega a una indeterminacion del tipo | ||
| + | <math> | ||
| + | \frac{\infty}{\infty} | ||
| + | </math>. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Con este tipo de indeterminaciones tambien se puede utilizar la regla | ||
| + | [[Indeterminaciones#Procedimiento 2|regla de L'Hôpital]]. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ===Procedimiento 3=== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Si <math> | ||
| + | \mathrm{f} | ||
| + | </math> | ||
| + | y | ||
| + | <math> | ||
| + | \mathrm{g} | ||
| + | </math> | ||
| + | son polinomios y | ||
| + | <math> | ||
| + | x_0 | ||
| + | </math> | ||
| + | es mas o menos infinito, se puede proceder de la siguiente manera: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | #1. se divide ambos polinomios por la mayor potencia de <math> x </math> en el denominador y el numerador ( <math> x </math> elevado al mayor de los grados de ambos polinomios ) | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | #2. se simplifican las fracciones de potencias de <math> x </math>, y | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | #3. se hace tender <math> x </math> a <math> \infty </math>. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ===Ejemplo 4=== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \lim_{x \to \infty } \frac{x^2 - 1}{x^3 + x + 1} = | ||
| + | \lim_{x \to \infty } \frac{\frac{x^2}{x^3} - \frac{1}{x^3}}{\frac{x^3}{x^3} + | ||
| + | \frac{x}{x^3} + \frac{1}{x^3}} = | ||
| + | \lim_{x \to \infty } \frac{\frac{1}{x} - \frac{1}{x^3}}{1 + | ||
| + | \frac{1}{x^2} + \frac{1}{x^3}} = | ||
| + | </math> | ||
| + | </center> | ||
| + | <center> | ||
| + | <math> | ||
| + | = \frac{\displaystyle \lim_{x \to \infty} \left( \, \frac{1}{x} - \frac{1}{x^3} | ||
| + | \, \right)}{\displaystyle \lim_{x \to \infty } \left( \, 1 + | ||
| + | \frac{1}{x^2} + \frac{1}{x^3} \, \right)} = \frac{0 + 0}{1 + 0 + 0} = 0 | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | Observese que tanto el denominador como el numerador de | ||
| + | <center> | ||
| + | <math> | ||
| + | \frac{x^2 - 1}{x^3 + x + 1} | ||
| + | </math> | ||
| + | </center> | ||
| + | tienden a | ||
| + | <math> | ||
| + | \infty | ||
| + | </math> | ||
| + | cuando | ||
| + | <math> | ||
| + | x | ||
| + | </math> | ||
| + | tiende a | ||
| + | <math> | ||
| + | \infty | ||
| + | </math>. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Calculemos de nuevo el mismo limite utilizando la regla de L'Hôpital | ||
| + | <center> | ||
| + | <math> | ||
| + | \lim_{x \to \infty } \frac{x^2 - 1}{x^3 + x + 1} = | ||
| + | \lim_{x \to \infty } \frac{2x}{3x^2 + 1}} = \lim_{x \to \infty } \frac{2}{6x} = 0 | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ==Indeterminación del tipo 0 por infinito== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Este tipo de indeterminaciones se tranforman en indeterminaciones de alguno de | ||
| + | los dos tipos vistos anteriormente ([[Indeterminaciones#Indeterminaciones del tipo 0/0|0/0]] y | ||
| + | [[Indeterminaciones#Indeterminaciones del tipo infinito/infinito|infinito/infinito]]). | ||
| + | |||
| + | Si | ||
| + | <math> | ||
| + | \lim_{x \to x_0} \mathrm{f} \left( \, x \, \right) = 0 | ||
| + | </math> | ||
| + | | ||
| + | y | ||
| + | | ||
| + | <math> | ||
| + | \lim_{x \to x_0} \mathrm{g} \left( \, x \, \right) = \infty | ||
| + | </math>, | ||
| + | entonces el limite | ||
| + | <center> | ||
| + | <math> | ||
| + | \lim_{x \to x_0} \mathrm{g} \left( \, x \, \right) \cdot \mathrm{f} \left( \, x \, \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | se puede reescribir de la siguiente manera: | ||
| + | <center> | ||
| + | <math> | ||
| + | \lim_{x \to x_0} \frac{\mathrm{g} \left( \, x \, \right)}{\frac{1}{\mathrm{f} \left( \, x \, \right)}} | ||
| + | </math> | ||
| + | </center> | ||
| + | con lo cual se llegaria a una indeterminacion del tipo | ||
| + | <math> | ||
| + | \frac{\infty}{\infty} | ||
| + | </math> | ||
| + | dado que | ||
| + | <center> | ||
| + | <math> | ||
| + | \lim_{x \to \infty}\frac{1}{\mathrm{f} \left( \, x \, \right)} = \infty | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | |||
| + | <br/> | ||
| + | |||
| + | Alternativamente el limite | ||
| + | <center> | ||
| + | <math> | ||
| + | \lim_{x \to x_0} \mathrm{f} \left( \, x \, \right) = 0 | ||
| + | </math> | ||
| + | </center> | ||
| + | se puede poner como | ||
| + | <center> | ||
| + | <math> | ||
| + | \lim_{x \to x_0} \frac{\mathrm{f} \left( \, x \, \right)}{\frac{1}{\mathrm{g} \left( \, x \, \right)}} | ||
| + | </math> | ||
| + | </center> | ||
| + | con lo cual se llegaria a una indeterminacion del tipo | ||
| + | <math> | ||
| + | \frac{0}{0} | ||
| + | </math> | ||
| + | dado que | ||
| + | <center> | ||
| + | <math> | ||
| + | \lim_{x \to \infty}\frac{1}{\mathrm{g} \left( \, x \, \right)} = 0 | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| - | + | [[Categoría:Matemáticas]] | |
Revisión actual
Tabla de contenidos |
Introducción
Muchas de las funciones elementales que se ven en bachillerato son continuas en toda la recta real o en casi todos los puntos de su dominio.
Las funciones elementales son aquellas que se utilizan para construir otras funciones mediante las operaciones con funciones: suma, resta, división, multiplicación, composición, etc.
Son funciones elementales los polinomios, las funciones exponenciales
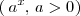 , el coseno, el seno, etc.
, el coseno, el seno, etc.
Si una función
 es continua en
es continua en
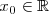 ,
el limite de
,
el limite de
 cuando
cuando
 tiende a
tiende a
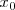 se puede calcular simplemente evaluando
se puede calcular simplemente evaluando
 en
en
 .
.
Ejemplo 0
Como
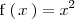 es una función continua en todo
es una función continua en todo
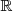 se tiene que
se tiene que
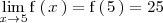
Indeterminación del tipo 0/0
En muchos casos, el limite se calcula utilizando las propiedades de los limites.
Por ejemplo, si existen los limites
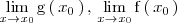
y
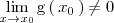
entonces se puede calcular el límite
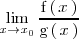
dividiendo
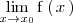 entre
entre
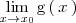 :
:
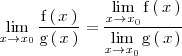
¿Pero que sucede cuando
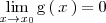 ?
?
Pueden darse dos casos:
- 1.
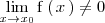 , o bien
, o bien
- 2.
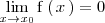 .
.
En este último caso, de existir el limite
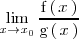
se ha de calcular de otra manera.
Procedimiento 1
Si  y
y
 son polinomios, entonces se puede dividir ambos por
son polinomios, entonces se puede dividir ambos por
 ,
cuantas veces sea posible.
,
cuantas veces sea posible.
Ejemplo 1
Calculemos el limite
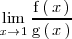
con
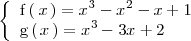
Ambos polinomios,
 y
y
 ,
se anulan en
,
se anulan en
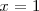 ,
por lo tanto ambos son divisibles por
,
por lo tanto ambos son divisibles por
 .
.
Si dividimos
 y
y
 por
por
 una vez y luego otra, nos queda que
una vez y luego otra, nos queda que
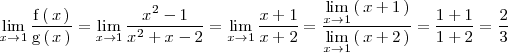
Todas esas divisiones se puede hacer por la regla de Ruffini.
Procedimiento 2
Tanto si
 y
y
 son polinomios, como si no lo son, se puede utilizar la regla de L'Hôpital:
son polinomios, como si no lo son, se puede utilizar la regla de L'Hôpital:
Si existe
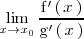
ya sea
 real, infinito o menos infinito, entonces
real, infinito o menos infinito, entonces
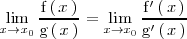
donde
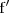 y
y
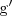 son las derivadas de
son las derivadas de
 y
y
 .
.
Ejemplo 2
Calculemos
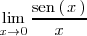
Como la funcion seno y la funcion identidad
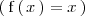 son funciones continuas, lo primero que hacemos es sustituir
son funciones continuas, lo primero que hacemos es sustituir
 por cero en
por cero en
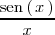
con lo que obtenemos la indeterminación
 .
.
Esto NO significa que el limite NO exista, de hecho si derivamos el numerador y
el denominador en
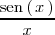 obtenemos
obtenemos
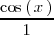 que cuando
que cuando
 tiende a
tiende a
 tiende a 1.
tiende a 1.
Por lo tanto, por la regla de L'Hôpital
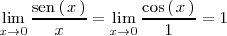
El ultimo límite se calcula teniendo en cuenta que la función coseno es continua
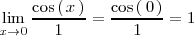
Ejemplo 3
Calculemos el limite del ejemplo 1 utilizando la regla de L'Hôpital y comprobemos que el resultado es el mismo que obtuvimos utilizando el procedimiento 1.
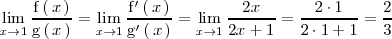
Indeterminación del tipo infinito/infinito
Supongamos que queremos calcular el limite de
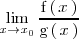
y que
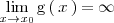 .
.
Puede darse dos casos, o bien:
- 1.
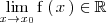 , o bien
, o bien
- 2.
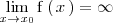 .
.
En el primer caso
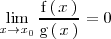 .
.
En este segundo caso se dice que se tiene una indeterminación del tipo
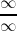 .
.
Veamos a continuación diferentes metodos de calcular limites cuando
se llega a una indeterminacion del tipo
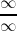 .
.
Con este tipo de indeterminaciones tambien se puede utilizar la regla regla de L'Hôpital.
Procedimiento 3
Si  y
y
 son polinomios y
son polinomios y
 es mas o menos infinito, se puede proceder de la siguiente manera:
es mas o menos infinito, se puede proceder de la siguiente manera:
- 1. se divide ambos polinomios por la mayor potencia de
 en el denominador y el numerador (
en el denominador y el numerador (  elevado al mayor de los grados de ambos polinomios )
elevado al mayor de los grados de ambos polinomios )
- 2. se simplifican las fracciones de potencias de
 , y
, y
- 3. se hace tender
 a
a 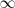 .
.
Ejemplo 4
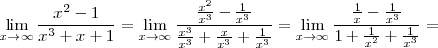
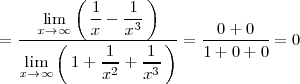
Observese que tanto el denominador como el numerador de
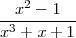
tienden a
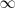 cuando
cuando
 tiende a
tiende a
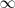 .
.
Calculemos de nuevo el mismo limite utilizando la regla de L'Hôpital
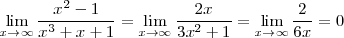
Indeterminación del tipo 0 por infinito
Este tipo de indeterminaciones se tranforman en indeterminaciones de alguno de los dos tipos vistos anteriormente (0/0 y infinito/infinito).
Si
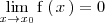 y
y
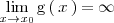 ,
entonces el limite
,
entonces el limite
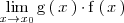
se puede reescribir de la siguiente manera:
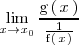
con lo cual se llegaria a una indeterminacion del tipo
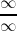 dado que
dado que
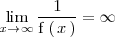
Alternativamente el limite
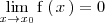
se puede poner como
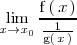
con lo cual se llegaria a una indeterminacion del tipo
 dado que
dado que