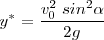Composición de movimientos
De Wikillerato
| (6 ediciones intermedias no se muestran.) | |||
| Línea 6: | Línea 6: | ||
| - | La intención del nadador es atravesar el río de modo perpendicular a las orillas. De hecho, si tomara un objeto en la otra orilla como referencia, justo enfrente del lugar desde donde se lanzaría al agua, para llegar a ese punto, se vería a realizar un esfuerzo contra la corriente y | + | La intención del nadador es atravesar el río de modo perpendicular a las orillas. De hecho, si tomara un objeto en la otra orilla como referencia, justo enfrente del lugar desde donde se lanzaría al agua, para llegar a ese punto, se vería obligado a realizar un esfuerzo contra la corriente y nadar con sus brazos de modo oblicuo. En caso contrario sus brazadas le llevarán a un lugar de la orilla opuesta río abajo, más o menos abajo en función de la velocidad de la corriente y del tiempo que tardase en atravesar el río. Su dirección sería la de la resultante de la propia velocidad y de la de la corriente. |
Para este movimiento tendríamos una ecuación: | Para este movimiento tendríamos una ecuación: | ||
| Línea 28: | Línea 28: | ||
<math>v_x = v_0\cos\alpha</math> y <math>v_x = v_0\sin\alpha - gt</math> | <math>v_x = v_0\cos\alpha</math> y <math>v_x = v_0\sin\alpha - gt</math> | ||
| - | <math>x = v_0\cos\alpha t</math> y <math>y = v_0\sin\alpha t - \frac{1}{2}gt^2</math> | + | <math>x = v_0\cos\alpha\, t</math> y <math>y = v_0\sin\alpha\, t - \frac{1}{2}gt^2</math> |
A estas ecuaciones se les llama ecuaciones paramétricas del movimiento, pues ambas coordenadas, <math>x</math> e <math>y</math>, son función del parámetro <math>t</math>. | A estas ecuaciones se les llama ecuaciones paramétricas del movimiento, pues ambas coordenadas, <math>x</math> e <math>y</math>, son función del parámetro <math>t</math>. | ||
| Línea 36: | Línea 36: | ||
Si eliminamos el tiempo entre las dos últimas ecuaciones paramétricas, se obtiene | Si eliminamos el tiempo entre las dos últimas ecuaciones paramétricas, se obtiene | ||
| - | <math> y = x \tan\alpha- \frac{1}{2} \frac{x^2}{ v_0^2\ cos^2\ alpha}</math> | + | <math> y = x \tan\alpha- \frac{1}{2} \frac{x^2}{ v_0^2\ cos^2\alpha}</math> |
De las ecuaciones paramétricas se puede deducir: | De las ecuaciones paramétricas se puede deducir: | ||
| Línea 42: | Línea 42: | ||
'''Altura y alcances máximos:''' | '''Altura y alcances máximos:''' | ||
| - | La altura máxima <math>y^{*}</math> corresponde al punto donde <math>v_y = 0</math>, es decir <math>0 = | + | La altura máxima <math>y^{*}</math> corresponde al punto donde <math>v_y = 0</math>, es decir <math>0 = v_0 \sin \alpha - g t</math>, de donde |
<math> t = \frac{ v_0 \sin\alpha }{ g }</math> | <math> t = \frac{ v_0 \sin\alpha }{ g }</math> | ||
| Línea 54: | Línea 54: | ||
multiplicando y dividiendo por 2 | multiplicando y dividiendo por 2 | ||
| - | <math> x = \frac{ | + | <math> x = \frac{v_0^2\ sin{2\alpha}} { 2 g }</math> |
Esta es la abcisa que corresponde a la altura máxima <math>y^{*}</math> , teniendo en cuenta que la parábola es una curva simétrica con respecto al vértice, tendremos que el alcance máximo <math>x^{*}</math> será el doble del de la y máxima, por lo tanto | Esta es la abcisa que corresponde a la altura máxima <math>y^{*}</math> , teniendo en cuenta que la parábola es una curva simétrica con respecto al vértice, tendremos que el alcance máximo <math>x^{*}</math> será el doble del de la y máxima, por lo tanto | ||
| - | <math> | + | <math> x^{*} = \frac{ v_0^2\sin 2\alpha} { g }</math> |
| - | Para conocer la <math>y^{*}</math> nos bastará sustituir el t correspondiente en la ecuación paramétrica de la y: | + | Para conocer la <math>y^{*}</math> nos bastará sustituir el <math>t</math> correspondiente en la ecuación paramétrica de la y: |
| - | <math> y^{*} = v_0 \sin\alpha \frac { | + | <math> y^{*} = v_0 \sin\alpha \frac{ v_0 \sin\alpha}{ g } - \frac {1}{2} g \left (\frac{ v_0 \sin\alpha }{g}\right )^2</math> |
| - | Con lo cual <math> y^{*} = frac{ v_0^2\ sin^2\ alpha}{ 2 g }</math> | + | Con lo cual <math> y^{*} = \frac{ v_0^2\ sin^2\alpha}{ 2 g }</math> |
[[Category:Física]] | [[Category:Física]] | ||
Revisión actual
Composición de movimientos rectilíneos y uniformes
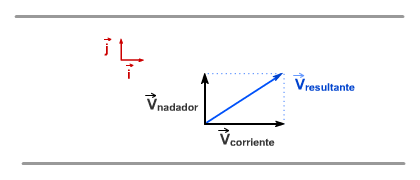
En la vida práctica se trataría del movimiento que sigue un nadador que atraviesa un río, de orilla a orilla, de corriente muy suave en ausencia de remolinos.
La intención del nadador es atravesar el río de modo perpendicular a las orillas. De hecho, si tomara un objeto en la otra orilla como referencia, justo enfrente del lugar desde donde se lanzaría al agua, para llegar a ese punto, se vería obligado a realizar un esfuerzo contra la corriente y nadar con sus brazos de modo oblicuo. En caso contrario sus brazadas le llevarán a un lugar de la orilla opuesta río abajo, más o menos abajo en función de la velocidad de la corriente y del tiempo que tardase en atravesar el río. Su dirección sería la de la resultante de la propia velocidad y de la de la corriente.
Para este movimiento tendríamos una ecuación:
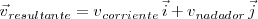
de modo que el módulo de la velocidad resultante viene dado por:
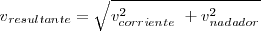
Composición de un movimiento rectilíneo y uniforme con un movimiento rectilíneo uniformemente acelerado perpendicular al anterior
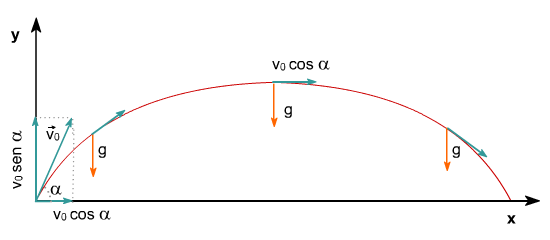
Consideremos el lanzamiento de una partícula sometida al campo gravitatorio terrestre, que consideraremos siempre vertical e igual a 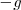 . La velocidad de la partícula forma un ángulo
. La velocidad de la partícula forma un ángulo 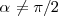 con la horizontal en el instante del lanzamiento.
con la horizontal en el instante del lanzamiento.
Nosotros podremos abordar el estudio del movimiento de la partícula como el resultado de la suma geométrica de un movimiento rectilíneo y uniforme sobre el eje 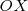 y un movimiento rectilíneo uniformemente acelerado, con aceleración igual a
y un movimiento rectilíneo uniformemente acelerado, con aceleración igual a 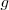 que se desarrolla sobre el eje
que se desarrolla sobre el eje 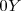 .
.
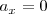 y
y 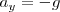
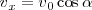 y
y 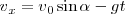
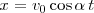 y
y 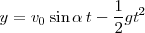
A estas ecuaciones se les llama ecuaciones paramétricas del movimiento, pues ambas coordenadas,  e
e 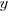 , son función del parámetro
, son función del parámetro  .
.
Si eliminamos el tiempo entre las dos últimas ecuaciones paramétricas, se obtiene
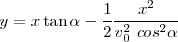
De las ecuaciones paramétricas se puede deducir:
Altura y alcances máximos:
La altura máxima 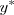 corresponde al punto donde
corresponde al punto donde 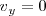 , es decir
, es decir 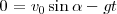 , de donde
, de donde
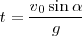
Sustituyendo este valor de  en la ecuación de
en la ecuación de 
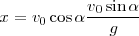
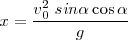
multiplicando y dividiendo por 2
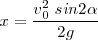
Esta es la abcisa que corresponde a la altura máxima 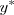 , teniendo en cuenta que la parábola es una curva simétrica con respecto al vértice, tendremos que el alcance máximo
, teniendo en cuenta que la parábola es una curva simétrica con respecto al vértice, tendremos que el alcance máximo 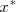 será el doble del de la y máxima, por lo tanto
será el doble del de la y máxima, por lo tanto
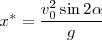
Para conocer la 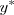 nos bastará sustituir el
nos bastará sustituir el  correspondiente en la ecuación paramétrica de la y:
correspondiente en la ecuación paramétrica de la y:
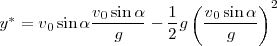
Con lo cual