Caída libre y lanzamiento vertical
De Wikillerato
| (77 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| - | + | == Caída libre == | |
| - | + | La '''caída libre''' es un caso particular del [[Movimiento rectilíneo uniformemente acelerado| movimiento rectilíneo uniformemente acelerado]], en el cual la [[aceleración]] es<math> -g</math> siendo <math> g = - \vec g\ </math> | |
| - | + | En consecuencia, las ecuaciones del movimiento serán: | |
| - | <math> v = v_0 | + | |
| + | Para el caso de la caída libre, la velocidad inicial es cero; la propia frase lo indica: ''se deja caer el cuerpo en caída libre''. | ||
| + | |||
| + | <math>v = v_0 - g t</math> como <math>v_0 = 0</math>, queda <math>v = – g t</math> | ||
Por otra parte, para el espacio, o altura a la que se encuentra el cuerpo: | Por otra parte, para el espacio, o altura a la que se encuentra el cuerpo: | ||
| Línea 10: | Línea 13: | ||
<math> y = y_0 + v_0 t - \frac {1}{2} g t^2</math> | <math> y = y_0 + v_0 t - \frac {1}{2} g t^2</math> | ||
| - | <math> y = y_0 - \frac {1}{2}g t^2</math> | + | <math> y = y_0 - \frac {1}{2} g t^2</math> |
| - | + | La representación gráfica del movimiento será: | |
| - | + | [[Imagen:Caida_libre.gif]] | |
| - | |||
| - | <math> y = y_0 + v_0 t - \frac {1}{2} g t^2</math> | + | |
| + | |||
| + | == Lanzamiento vertical == | ||
| + | |||
| + | Para el '''lanzamiento vertical''' nos encontramos con que <math>v_0</math> es positiva, y así se mantendrá aún cuando su módulo llegue a valer cero. Esto ocurrirá en el punto más alto de la trayectoria, en el cual la <math>v = 0</math>, pues pasará de valores positivos a negativos. En ese punto de la altura máxima, el móvil se encontrará parado durante un instante, después del cual comenzará caer. Durante todo el movimiento la aceleración que sufrirá la partícula será la de la gravedad, la cual siempre tiene el mismo sentido, hacia abajo y, por convenio, negativo. | ||
| + | |||
| + | <math>v = v_0 - g t</math> | ||
| + | |||
| + | <math> y = y_0 + v_0 t - \frac {1}{2} g t^2 </math> | ||
| + | |||
| + | La representación gráfica del movimiento será: | ||
| + | |||
| + | [[Imagen:grafica_lanzamiento_vertical.gif]] | ||
| + | |||
| + | Para <math>t^*</math>, la tangente a la gráfica <math>y-t</math> es horizontal, se corresponde con la altura máxima y con el instante en que la gráfica <math>v-t</math> se hace cero. | ||
| + | |||
| + | == Véase también == | ||
| + | |||
| + | : [[Movimiento circular uniforme]] | ||
| + | |||
| + | |||
| + | [[Category:Física]] | ||
Revisión actual
Caída libre
La caída libre es un caso particular del movimiento rectilíneo uniformemente acelerado, en el cual la aceleración es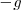 siendo
siendo 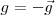
En consecuencia, las ecuaciones del movimiento serán:
Para el caso de la caída libre, la velocidad inicial es cero; la propia frase lo indica: se deja caer el cuerpo en caída libre.
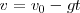 como
como 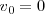 , queda
, queda 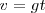
Por otra parte, para el espacio, o altura a la que se encuentra el cuerpo:
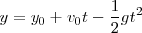
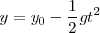
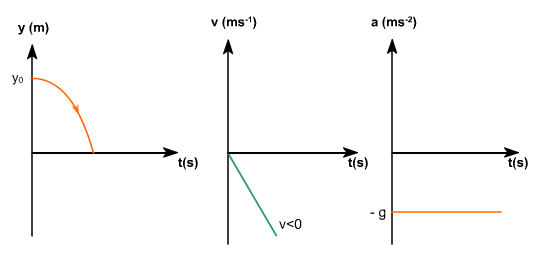
La representación gráfica del movimiento será:
Lanzamiento vertical
Para el lanzamiento vertical nos encontramos con que 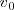 es positiva, y así se mantendrá aún cuando su módulo llegue a valer cero. Esto ocurrirá en el punto más alto de la trayectoria, en el cual la
es positiva, y así se mantendrá aún cuando su módulo llegue a valer cero. Esto ocurrirá en el punto más alto de la trayectoria, en el cual la 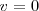 , pues pasará de valores positivos a negativos. En ese punto de la altura máxima, el móvil se encontrará parado durante un instante, después del cual comenzará caer. Durante todo el movimiento la aceleración que sufrirá la partícula será la de la gravedad, la cual siempre tiene el mismo sentido, hacia abajo y, por convenio, negativo.
, pues pasará de valores positivos a negativos. En ese punto de la altura máxima, el móvil se encontrará parado durante un instante, después del cual comenzará caer. Durante todo el movimiento la aceleración que sufrirá la partícula será la de la gravedad, la cual siempre tiene el mismo sentido, hacia abajo y, por convenio, negativo.
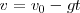
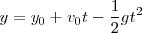
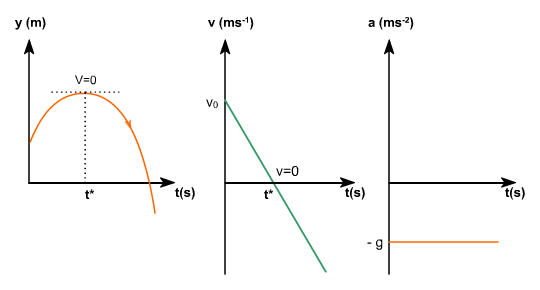
La representación gráfica del movimiento será:
Para 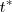 , la tangente a la gráfica
, la tangente a la gráfica 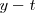 es horizontal, se corresponde con la altura máxima y con el instante en que la gráfica
es horizontal, se corresponde con la altura máxima y con el instante en que la gráfica  se hace cero.
se hace cero.