Navegación
Movimiento rectilíneo
De Wikillerato
(→Representaciones gráficas) |
|||
| (32 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| - | + | {{en desarrollo}} | |
| - | Llamamos | + | Llamamos '''movimiento rectilíneo y uniforme''' al movimiento de un punto material que recorre espacios iguales en tiempos iguales. Dado que hemos definido la [[Concepto de velocidad| velocidad]] como la variación del vector posición con relación al tiempo, en este tipo de [[Estudio_del_movimiento_de_un_cuerpo| movimiento]] la velocidad será constante: |
<math>\vec v = \frac {\Delta r}{\Delta t} = \frac {\vec r_2 - \vec r_1 }{ t_2 - t_1 } </math> | <math>\vec v = \frac {\Delta r}{\Delta t} = \frac {\vec r_2 - \vec r_1 }{ t_2 - t_1 } </math> | ||
| - | En el caso unidimensional, si queremos establecer la ecuación que nos dé la posición del punto material, <math>x</math>, en un instante cualquiera <math>t</math>, sabiendo que la posición inicial es <math>x_0</math> | + | En el caso unidimensional, si queremos establecer la ecuación que nos dé la posición del punto material, <math>x</math>, en un instante cualquiera <math>t</math>, sabiendo que la posición inicial es <math>x_0</math> para el instante<math> t = 0</math>, tendremos: |
<math> v = \frac {\Delta x}{\Delta t} = \frac {x - x_0 }{ t - t_0} </math> | <math> v = \frac {\Delta x}{\Delta t} = \frac {x - x_0 }{ t - t_0} </math> | ||
| Línea 13: | Línea 13: | ||
<math> x = x_0 + v (t - t_0)</math> | <math> x = x_0 + v (t - t_0)</math> | ||
| - | Vemos que obtenemos para <math>x</math> una función lineal de <math>t</math>, en la cual v es el coeficiente de la variable independiente <math>t</math> y <math>x_0</math> es la abcisa para el instante <math>t = | + | Vemos que obtenemos para <math>x</math> una función lineal de <math>t</math>, en la cual v es el coeficiente de la variable independiente <math>t</math> y <math>x_0</math> es la abcisa para el instante <math>t = t_0</math>. |
| + | |||
| + | |||
| + | == Representaciones gráficas == | ||
| + | |||
| + | Teniendo en cuenta que la representación de una función lineal es una recta cuya pendiente es el coeficiente de la variable, es decir, en este caso la velocidad, obtenemos: | ||
| + | |||
| + | == Véase también == | ||
| + | : [[Estudio del movimiento de un cuerpo]] | ||
| + | |||
| + | : [[Movimiento rectilíneo uniformemente acelerado]] | ||
| + | |||
| + | : [[Caída libre y lanzamiento vertical]] | ||
| + | |||
| + | : [[Movimiento circular uniforme]] | ||
| + | |||
| + | : [[Composición de movimientos]] | ||
| + | |||
| + | [[Category:Física]] | ||
Revisión actual
Uno o más usuarios están trabajando actualmente en extender este artículo.
Es posible que, a causa de ello, haya lagunas de contenido o deficiencias de formato. Por favor, antes de realizar correcciones mayores o reescrituras, contacta con ellos en la página de discusión.
Llamamos movimiento rectilíneo y uniforme al movimiento de un punto material que recorre espacios iguales en tiempos iguales. Dado que hemos definido la velocidad como la variación del vector posición con relación al tiempo, en este tipo de movimiento la velocidad será constante:
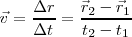
En el caso unidimensional, si queremos establecer la ecuación que nos dé la posición del punto material, 
, en un instante cualquiera 
, sabiendo que la posición inicial es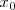 
para el instante
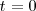, tendremos:
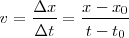
de donde,
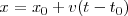
Vemos que obtenemos para una función lineal de , en la cual v es el coeficiente de la variable independiente y 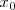es la abcisa para el instante 
.
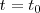Representaciones gráficas
Teniendo en cuenta que la representación de una función lineal es una recta cuya pendiente es el coeficiente de la variable, es decir, en este caso la velocidad, obtenemos:
